虹吸離心機回轉組件模態(tài)分析

蒯念生　陳　志　李建明　歐鳳蘭　馬　維

(四川大學)

    摘要：應用有限元方法,建立了由轉鼓、主軸和皮帶輪組成的虹吸離心機回轉組件有限元模型,并進行模態(tài)分析。結果表明,對其主軸采用不同的約束支承,得到的臨界轉速有較大差異;提取回轉組件在轉鼓空轉和滿載工作條件下的模態(tài),得到其前3階固有頻率以及振型,其轉鼓滿載時回轉組件的臨界轉速比空轉時的略有降低。

    關鍵詞：虹吸離心機　模態(tài)分析　臨界轉速　有限元方法

    中圖分類號：TQ051·8+4　　　文獻標識碼　A　　　文章編號　0254-6094(2010)01-0036-04

    傳統(tǒng)的虹吸離心機臨界轉速計算方法是把離心機簡化成單自由度模型,同時考慮臂長效應、回轉效應和彈性支承的影響。由于做了大量的簡化,給計算帶來較大的誤差,往往得不到正確的結果[1]。應用有限元方法,采用實體單元建模,簡化相對較少,從而能保證結果的準確和可靠性。當前,有限元方法在離心機回轉組件的模態(tài)分析中得到了廣泛的應用。毛文貴等[2]運用VisuaNastran對臥螺離心機轉鼓進行了模態(tài)分析;王輝斌[3]運用ANSYS對翻袋式離心機的三軸系統(tǒng)進行了模態(tài)分析;顧威[4]運用ANSYS對臥螺離心機螺旋輸送器進行了模態(tài)分析。

    虹吸離心機是一種具有高效過濾性能的機種,其轉鼓結構比普通離心機的更為特殊,增加了臨界轉速傳統(tǒng)計算法的難度。本文應用有限元方法,建立了由轉鼓、主軸、皮帶輪組成的回轉組件有限元模型,并進行橫向振動模態(tài)分析。

    1　模態(tài)分析理論基礎

    研究系統(tǒng)的固有頻率,需要求解系統(tǒng)的動力特征方程。在小變形條件下,可采用振型疊加法進行求解。計算方法采用求解不考慮阻尼影響的系統(tǒng)自由振動方程[5, 6],即:

    [M]{¨u}+[K]{u}={0} (1)

    式中　{¨u}———節(jié)點的加速度向量,m/s2;

    {u}———節(jié)點的位移向量,m;

    [M]———質量矩陣, kg;

    [K]———剛度矩陣,N/m。

    它的解可以假設為以下形式:

    求解此式就可以求得系統(tǒng)的各階固有頻率,也就是軸發(fā)生共振的各階臨界轉速。在分析時采用Block Lanczos算法、稀疏矩陣來求解廣義特征值問題,從而提取虹吸離心機回轉組件的多階模態(tài)。此法具有如下的優(yōu)點:

    a.計算精度高,速度快,在工程中得到廣泛應用;

    b.需提取對稱特性模型很多階振型時,此方法很有效;

    c.在有限元模型中允許有質量較差的實體單元;

    d.可以有效地處理約束方程;

    e.可以很好地處理剛度模型。

    2　有限元模型的建立

    2.1　模型的建立與簡化

    首先,建立由轉鼓、主軸和皮帶輪組成的虹吸離心機回轉組件模型,定義回轉組件的材料為不銹鋼,其彈性模量E為205. 8G Pa,泊松比ν為0. 3,密度ρ0為7 850 kg/m3。為了縮短計算時間,精簡網格,對虹吸離心機轉鼓的倒角、轉鼓底部的開孔進行簡化,對皮帶輪進行一定的簡化,帶輪的輪槽和輻板結構不予考慮。

    由于回轉組件的對稱性,文中先建立其二維模型,并用PLANT42單元進行網格劃分,然后將單元網格繞其旋轉軸旋轉360°,并通過定義使模型由二維PLANT42單元轉化為三維SOLID45單元,圖1為虹吸離心機回轉組件的實體和有限元模型。

    影響結構動力特性的因素有4個:結構阻尼、質量、剛度和邊界條件。模態(tài)分析與結構所受的載荷作用無關。但如果預應力載荷引起結構剛度的變化或者構件性質的改變(如溫度變化引起的彈性模量的改變),那么就必須考慮預應力的影響。由于文中回轉組件所受載荷對結構剛度和性質的改變不大,故不考慮預應力載荷的影響。

    2.2　約束的施加

    2.2.1　軸承為剛性約束時邊界條件的處理把軸承視作剛性約束時,在軸上對應軸承位置的節(jié)點上施加徑向約束,在軸肩處施加軸向約束。

    2.2.2　軸承為彈性約束時邊界條件的處理考慮到軸承支承的彈性特征,將軸承簡化為彈簧[7, 8]。軸承的剛度為在一定預緊力下的剛度。高速下由于離心力的作用,軸承的剛度會降低,然而由于軸承的發(fā)熱量隨著轉速的升高而變大,可以補償一定的剛度損失,因此可忽略剛度隨轉速升高的降幅[9]。一般彈性約束的剛度值為108N/m[7],由文獻[10]可計算出軸承的剛度約為2×1010N/m。

    3　結果與分析

    回轉組件的振動有橫向(垂直于轉子軸線方向)、軸向及扭轉振動,或是幾種方式的組合。由于轉子質量不平衡離心力常是橫向的,且轉子橫向抗彎剛度較小,因此文中主要分析橫向彎曲振動,得到其振型及頻率,進行模態(tài)分析后提取了離心機回轉組件在不同約束條件下的一階固有頻率與臨界轉速,見表1。

    由表1可知,在對回轉組件進行模態(tài)分析時,如果把軸的支承簡化成剛性的,則其臨界轉速相對與彈性支承有較大幅度的增大。但根據實際結構情況,軸的支承并非剛性,軸承座和滾動軸承中的油膜都是彈性體,其剛度不能為假設的無窮大,支承剛度越小,臨界轉速越低。因此,把軸的支承簡化為剛性支承會造成較大的誤差。

    下面將應用彈簧單元的彈性約束,重點考察回轉組件在空轉和滿載運轉時的振動特性。

    3.1　轉鼓空轉時的振動特性

    考慮對于工程實際問題,沒有必要計算出全部的特征值。因此,文中只考察回轉組件前3階的振動特性。回轉組件在空轉時前3階的頻率與臨界轉速見表2。

    模態(tài)分析實質就是振型分析,分析的結果應該是位移的相對值而不是實際值,也就是說振型反映的雖然是位移特性,但不是位移。振型反映的是各質點的位移之間的比例關系。下面對回轉組件空載時前3階模態(tài)的相對位移進行考察。為了對回轉組件振型的位移特性更加直觀的表達,文中將回轉組件變形放大40倍。回轉組件前3階相對位移如圖2~4所示。

    3.2　轉鼓滿載時的振動特性

    在考慮轉鼓滿載工作狀態(tài)時,把物料和回轉組件當作一個整體,將物料的質量根據密度轉換將轉鼓壁增厚(轉鼓外徑不變,內徑變小)。經過近似計算,文中將轉鼓壁增厚20 mm。回轉組件滿載時前3階的頻率與臨界轉速見表3。

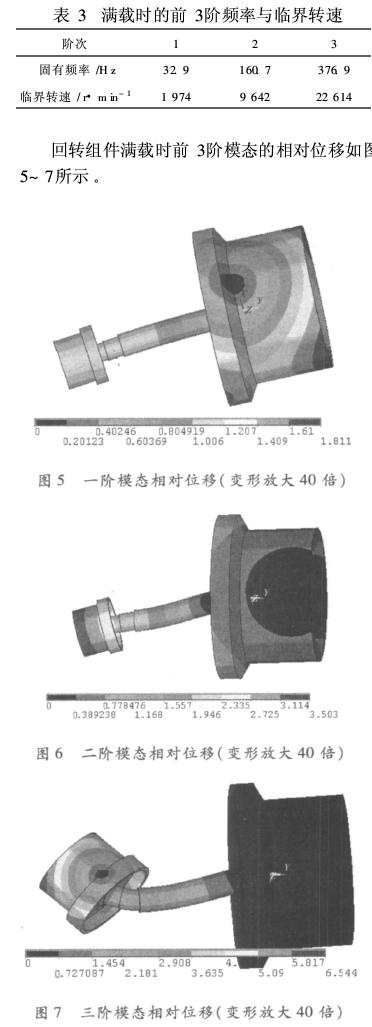
    由圖2~7可知,對于回轉組件的一階振型,轉鼓壁產生較大的相對位移變形,相對位移的最大值出現(xiàn)在轉鼓邊緣;對于二階振型,皮帶輪產生較大的相對位移變形,相對位移的最大值出現(xiàn)在皮帶輪的邊緣;對于三階振型,皮帶輪產生大的位移變形,主軸彎曲較為明顯,相對位移的最大值出現(xiàn)在皮帶輪的邊緣。隨著階數的增加,相對位移的最大值有較為顯著的增大。

    與空載相比,滿載時一階頻率略有降低(從36. 9Hz降低到32. 9 Hz);二階頻率和三階頻率略有增加(二階頻率從160. 5 Hz增加到160. 7Hz,三階頻率從372. 9 Hz增加到376. 9 Hz);轉鼓滿載時一階振型相對位移有所降低,二階振型相對位移略為增加,而三階振型的相對位移基本上保持不變。

    4　結論

    4.1　運用有限元方法,建立了由轉鼓、主軸、皮帶輪組成的虹吸離心機回轉組件有限元模型,進行模態(tài)分析。由于有限元分析采用3D實體單元,并且模型考慮了皮帶輪的影響,簡化相對較少,從而保證結果的準確和可靠性。

    4.2　采用Block Lanczos算法,對虹吸離心機回轉組件進行模態(tài)分析。分析發(fā)現(xiàn)對其主軸采用不同的約束支承,得到的臨界轉速有較大差異。采用彈性支承,臨界轉速明顯降低。因此,準確選擇彈性支承的剛度是正確預測臨界轉速的關鍵。

    4.3　分別考察了虹吸離心機回轉組件空轉和滿載運轉工況下前3階的振動特性。分析發(fā)現(xiàn),隨著階數的增加,回轉組件的相對位移有顯著增加。此外,與空載時相比,轉鼓滿載時一階頻率略有降低,二階頻率和三階頻率略有增加;一階振型相對位移有所降低,二階振型相對位移略為增加,而三階振型的相對位移基本上保持不變。

    參考文獻

    1　李自光,毛文貴,傅彩明.臥螺離心機轉鼓的應力應變有限元仿真分析.食品與機械, 2006, 22 (1): 62~65

    2　毛文貴,傅彩明.基于虛擬樣機技術的離心機轉鼓模態(tài)仿真研究.礦山機械, 2007, 35(1): 74~76

    3　王輝斌.翻袋式離心機旋轉部件的應力和振動分析:[碩士論文].北京:北京化工大學, 2001

    4　顧威.臥式螺旋卸料沉降離心機的螺旋強度和振動分析: [碩士論文].北京:北京化工大學, 2002

    5　倪振華.振動力學.西安:西安交通大學出版社, 1994

    6　仇偉德.機械振動.北京:北京石油大學出版社, 2001

    7　鐘佩思,孫雪顏,蘇超.基于ANSYS的鼓風機軸模態(tài)分析與仿真.煤礦機械, 2007, 28(10): 57~58

    8　李守仁,丁燕芳,王克義.某直升機旋翼動平衡試驗臺主軸動態(tài)分析.哈爾濱工程大學學報, 2004, 25(5):592~596

    9　Lin ChiweiTu J F,Kamman J.An Integrated Thermo-Me-chanical-Dynamic

 Model to Characterize Motorized Ma-chine ToolSpindlesDuringVeryHigh Speed

Rotation. In-ternational Journal of Machine Tools & Manufacture,2003, 43(10): 1035~1050

    10　陳忠.滾動軸承及其支承的剛度計算.煤礦機械,2006, 27(3): 387~388