臥螺離心機流場的三維數值模擬
臥螺離心機流場的三維數值模擬
鄭勝飛1, 2,任 欣1, 2,謝林君1, 2
(1.浙江工業大學過程裝備與控制工程研究所,浙江杭州 310032; 2.浙江工業大學機械制造及自動化教育部重點實驗室,浙江杭州 310032)
摘要:針對臥螺離心機理論研究的不足之處,采用Fluent軟件中的RSM模型和DPM模型模擬臥螺離心機三維流場,通過適當的求解策略,得到流場內的壓力分布和速度分布。結果表明,整個液環角速度滯后約為0. 83,模擬液壓約為理論值的65%,顆粒沉降時間與理論計算結果符合較好,為進一步深入研究奠定了基礎。
關鍵詞:化工機械;臥螺離心機;數值模擬;角速度滯后;顆粒沉降
中圖分類號:TQ051. 8 文獻標志碼:A 文章編號:1005-2895(2009)06-0026-04
0 引言
臥螺離心機是一種廣泛應用于石油、化工、冶金、醫藥、食品、輕工等行業的機械,既可以用于液相澄清,也可以用于固相脫水。由于離心分離過程的復雜性和多樣性,例如懸浮液的物理性能和濃度非常容易變化,特別是固相顆粒的大小形狀和運動的雜亂狀態帶來的問題,給理論和試驗研究造成了極大的難題。計算流體力學的發展,為臥螺離心機流場研究開辟了新的方向[1]1。在此基礎上,采用Fluent軟件對臥螺離心機流場進行數值模擬,研究了其流動規律和液-固分離特點。
1 模型簡化及網格創建
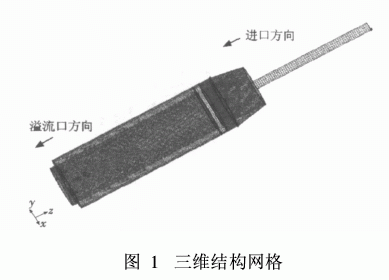
臥螺離心機中轉鼓和螺旋以一定的差轉速運行,實現懸浮液的分離及沉渣的排出。目前Fluent尚無直接對應的模型可進行模擬,因此本文對流域作了適當的簡化:未考慮螺旋的作用。主要計算尺寸如下:轉鼓長度L=800 mm,外直徑D=200 mm,液層深度h=2mm。采用定常方式計算流場, Fluent中高精度數值差分格式,例如二階迎風差格式,QUICK格式,主要針對于結構網格,應用于非結構網格效果并不理想。因此對于旋轉流動,要以少量計算時間取得較精確的數值模擬結果,須采用結構網格進行求解。將臥螺離心機的幾何結構劃分為多個子塊,針對每個子塊采用Cooper方法創建結構化網格,共得到66 434個網格、221 895個面、85 114個節點。在實體交界面處,重合邊界設置為Interface面。網格如圖1所示。
2 邊界條件及求解策略
2.1 邊界條件
入口設定為速度入口邊界,通過指定入口處的湍流強度和水力直徑來設定邊界條件,入口湍流強度按經驗公式[2]計算。臥螺離心機出口為溢流出口,出口處的壓力等于大氣壓,設定出口為壓力出口邊界條件。轉鼓壁設定為無滑移條件,轉鼓轉速設置為ω=39rad/s,對于自由液面處壁面,設置為有滑移。
2.2 求解策略
臥螺離心機內部流場屬于旋轉流動,流動較復雜,為獲取較精確解,計算過程中采用了以下求解步驟:1)壓力差值采用PRESTO!格式; 2)采用邊界網格自適應加密壁面附近網格; 3)改變壓力、速度的亞松馳參數,減少為0. 1; 4)使用步進解,首先計算沒有旋轉影響的流動,也就是說先在邊界條件中設定壁面為靜止壁面,至收斂后,再設置壁面速度,只求解動量方程至收斂,關閉湍流方程和雷諾應力方程,最后打開所有的方程獲取完全的耦合解; 5)在開始計算時,采用較低的旋轉速度,然后逐漸增加直至所需要的操作條件。
3 模擬結果分析[3-11]
3.1 壓力分布
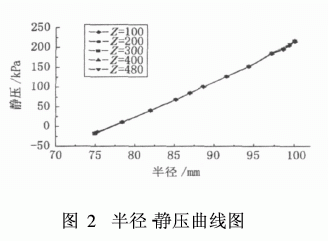
圖2是根據Z=100,Z=200,Z=300,Z=400,Z=580這5個截面沿半徑方向的靜壓力值繪制而成的。從圖上可以看出靜壓力沿著半徑方向從0增加到225 kPa,入口處及溢流口都與大氣相連,因此,在此二處的靜壓力接近零值。不同截面上的半徑-壓力關系基本趨于重合,說明靜壓力軸向梯度幾乎為零;對于徑向壓力分布,圖顯示壓力與半徑成拋物線關系,與臥螺離心機相對照的是,模擬所得靜壓即為離心機中存在的離心液壓。根據模擬結果可知,離心液壓為理論計算值的65. 6%左右,這對于離心機轉鼓強度優化設計具有一定的指導作用。
3.2 速度分布
圖3分別為轉鼓圓柱段3個不同階段的軸向速度折線圖,比較3個折線圖,可以把轉鼓內軸向流速分布規律劃分為3個階段。其中Z取粗略值可把400~600 mm歸為第1階段,由圖(a)可知,在流體剛進入轉鼓后,經過短暫的調整適應,流速分布呈現出一定的規律性,半徑在75~84 mm范圍內,流動沿Z軸負方向(即溢流口方向),在同一徑向液層深度上,隨著Z值變小,速度的絕對值不斷減小;在84~100 mm范圍內,流速沿Z軸正向,在同一Z處,沿半徑方向,速度先增大后減小至鼓壁處為零。由此可知,流速在此階段存在一個較大的回流。由于離心機平均軸向流速必定指向溢流口,因此圖形分布也顯示速度負方向的積分面積大于正方向。經過此階段后流動轉入第2階段(Z=200~400 mm),此階段速度分布均勻,從圖上看折線呈水平狀態。同時該階段也是較符合層流理論的階段。之后,流動接近溢流口,且存在轉鼓壁幾何結構的限制,流動發生了較大的變化,不再是層流流動狀態。Z在0~200 mm范圍屬于第3階段,該階段內流速方向與第1階段恰好相反,半徑在75~85 mm范圍內,流速為正, 85~100 mm范圍內,流速為負。
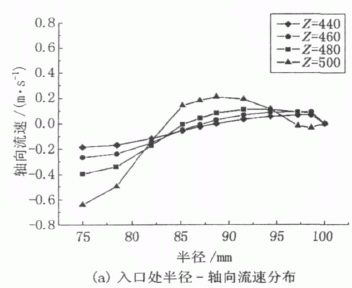
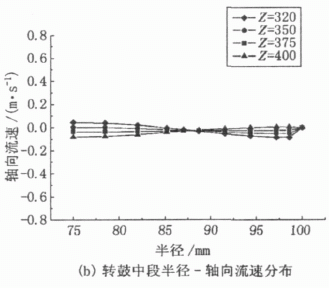
圖 3 不同階段軸速分布曲線
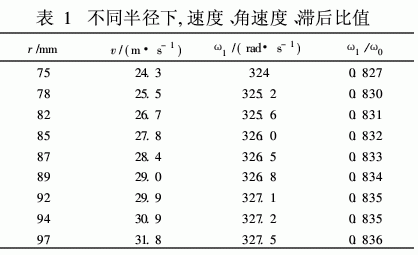
表1是根據模擬所得到切向速度,周向滯后比例與半徑的關系。本文中液層深度為25 mm,于是r/r2=0·75。根據文獻[1]47數據,可得出自由液面處ω/ω0的取值范圍為(0. 78~0. 91)。由于文獻中該作者并未指明自由液面層處a值是在直徑為多大的臥螺離心機中測定,也未指出轉鼓的轉速以及測量時的液層深度,因此只能進行定性的驗證。模擬中根據200mm臥螺離心機的處理量范圍,設定流量Q=4×10-4m3/s,遠小于文獻中的試驗流量,照常理推a值應當大于0. 91,可模擬求得a值為0.827。事實上文獻中角速度滯后曲線得出的理論前提為層流理論,即假定速度分量ur,uφ,uZ僅與半徑有關,而與φ,Z和時間t無關,且ur為0。而本文所進行的模擬則考慮了3者與φ和Z的關系,且認為運動為復雜的湍流流動,由此存在著一定的差距也不足為奇。同時,由于計算機運算能力的限制,以及偏微分方程的在離散過程中產生截斷誤差,也是造成誤差的原因之一。
3.3 顆粒相運動分析
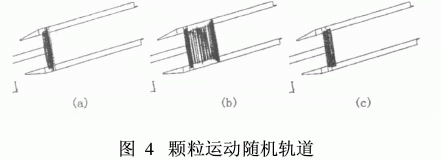
采用DPM模型加入顆粒相后,分析顆粒的運動軌跡。圖4為10μm顆粒在湍流作用下不同的運動軌跡。圖4(a)表明顆粒在離心力作用下很快就從自由液面運動到了轉鼓壁,圖4(b)顯示顆粒沿軸向運動較長時間后方沉降至轉鼓壁,圖4(c)中顆粒在足夠時間步長內陷入死循環而無法被分離。考慮到螺旋存在的影響,小直徑顆粒沉降所需時間較長,在碰到轉鼓壁之前,將先與螺旋葉片接觸,在軸向速度較小情況下,顆粒與螺旋發生碰撞反彈,從而對顆粒沉降產生不利影響。這種情況下,增大螺距,能同時提高沉渣輸送能力和提高分離效率,但螺旋升角太大,容易使渣周向打滑、堵塞、排渣困難。因此應當綜合考慮2者需求,以取合理值。
3.4 離心力場中顆粒沉降速度
液固2相的密度不同,使顆粒相對于液體存在1個徑向速度,從而實現2相的分離。在計算顆粒沉降速度時,首先要根據Ret判斷流型,而Ret中含有待求的ut,所以計算需要采用試差法。下表分別計算不同直徑顆粒在ω=324 rad/s,自由液面處顆粒的的沉降速度。
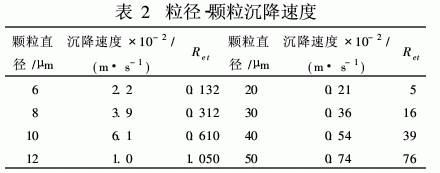
為了驗證Fluent計算顆粒運動的正確性,在表1的基礎上,計算出顆粒位于半徑R=100 mm處的理論沉降速度。將液環半徑除以最大和最小沉降速度,即可得到顆粒所需最小和最大沉降時間,并與模擬得到的沉降時間進行比較,見圖5。
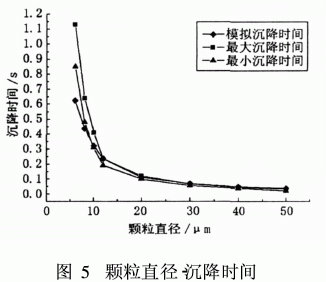
觀察圖5中3條曲線走向,可知顆粒直徑與沉降時間存在著二次曲線關系。直徑大于12μm以上的顆粒,模擬值與實際值吻合較好,可見Fluent關于顆粒計算符合斯托克斯公式。而6, 8, 10這3種顆粒存在不同程度的偏差。顆粒直徑越小,則偏差范圍愈大究其原因,可以發現在6μm時顆粒的沉降速度為2.×10-2m/s,當顆粒直徑下降至1μm時,沉降速度小至6. 1×10-4m/s。由于Fluent采用有限體積法求解方程,因此在偏微分方程組轉化為代數方程組后,不可避免地存在著截斷誤差。一方面,可以通過提高細化網格減少截斷誤差;另一方面由于計算機容量的限制提高網格將使得計算量成倍增加。隨著顆粒直徑的減小,當前計算條件下,將無法得到精確解。
4 結語
采用RSM模型和DPM模型對臥螺離心機兩相流場進行三維數值模擬,進一步明確了流場內各物理量的分布及液固分離機理。有如下結論:
1)在當前模擬結構條件下,所得離心液壓值約為理論計算值的65. 6%,這對于優化轉鼓結構能起到一定的指導作用。
2)沿轉鼓長度方向,軸向流速分布并不均勻,除在中間段與層流理論下的軸向速度分布較接近外,入口及溢流口處的流速分布皆變化較大。
3)轉鼓長度對對于大直徑顆粒分離影響不大,這時影響分離的主要原因是湍流及螺旋的攪動。
4)用Fluent軟件計算顆粒軌道,尤其對于小直徑顆粒的運動軌跡,還需要進一步提高網格精度和計算機運算能力,以獲得更精確計算結果。
參考文獻:
[1] 孫啟才,金鼎五.離心機原理結構與設計計算[M].北京:機械工業出版社, 1987.
[2] 王福軍.計算流體動力學分析: CFD軟件原理與應用[M].北京:清華大學出版社, 2004.
[3] 周強,程樂鳴,駱仲泱.方形臥式分離器兩相流場的數值模擬[J].動力工程, 2004, 24(4): 567-571.
[4] 耿麗萍,楊茉,曹瑋.高爐淤泥旋流法顆粒分離的數值模擬[J].工程熱物理學報, 2004, 25(4): 628-630.
[5] 趙斌娟,袁壽其,劉厚林.基于Mixture多相流模型計算雙流道泵全流道內固液兩相湍流[J].農業工程學報, 2008, 24(1): 7-12.
[6] 王春林,馬慶勇,李婷婷.攪拌漿液池固-液兩相流攪拌的數值模擬[J].排灌機械, 2007, 25(6): 38-41.
[7] 林瑋,王乃寧.旋風分離器內三維兩相流場的數值模擬[J].動力工程, 1999, 19(1): 72-76.
[8] 賴艷萍,賴維,盧曉江.圓柱型水力旋流器流場CFD軟件的數值模擬[J].輕工機械, 2007, 25(3): 20-22.
[9] 曹亞裙,陳建,王燦星,等.油煙機用多葉離心通風機內部流動的數值模擬[J].機電工程, 2009, 26(6): 38-40.
[10] 王衛國,周慎杰.圓柱旋流器多相流場的數值分析[J].化工裝備技術, 2006, 27(2): 17-19.
[11] 黃志新,錢才富,范德順.沉降離心機圓形轉鼓內液面速率的數值模擬[J].北京化工大學學報, 2007, 34(6): 645-648.[信息·簡訊]
標簽:
相關技術
2、如涉及作品內容、版權和其它問題,請在30日內與本網聯系,我們將在第一時間作出適當處理!有關作品版權事宜請聯系:+86-571-88970062