臥螺離心機(jī)旋轉(zhuǎn)部件振動(dòng)特性分析
臥螺離心機(jī)旋轉(zhuǎn)部件振動(dòng)特性分析
陽(yáng)文英,范德順
(北京化工大學(xué)機(jī)電工程學(xué)院,北京100029)
摘要:采用梁?jiǎn)卧謩e建立臥螺離心機(jī)轉(zhuǎn)鼓軸和螺旋軸的三維有限元模型,對(duì)其進(jìn)行ANSYS模態(tài)分析,將其結(jié)果與傳遞矩陣法計(jì)算結(jié)果進(jìn)行對(duì)比,結(jié)果基本一致,驗(yàn)證了ANSYS分析方法的可靠性,再將轉(zhuǎn)鼓軸模型和螺旋軸模型通過彈簧單元連接起來,進(jìn)行雙軸系統(tǒng)的模態(tài)分析,結(jié)果表明機(jī)器工作轉(zhuǎn)速遠(yuǎn)遠(yuǎn)小于一階臨界轉(zhuǎn)速,在正常工作轉(zhuǎn)速下,機(jī)器不會(huì)發(fā)生共振現(xiàn)象。
關(guān)鍵詞:臥螺離心機(jī);有限元;固有頻率
中圖分類號(hào):TQ051.8+4文獻(xiàn)標(biāo)識(shí)碼:A文章標(biāo)號(hào):1005-8265(2010)02-0011-03
引言
一般工廠中常見的機(jī)器都裝有旋轉(zhuǎn)部件即轉(zhuǎn)子,轉(zhuǎn)子連同它的軸承和支座統(tǒng)稱為轉(zhuǎn)子系統(tǒng)。離心機(jī)作為典型的旋轉(zhuǎn)機(jī)械,是以轉(zhuǎn)子作為工作主體的。當(dāng)機(jī)器運(yùn)轉(zhuǎn)時(shí),轉(zhuǎn)子系統(tǒng)常常發(fā)生振動(dòng),包括扭轉(zhuǎn)振動(dòng)和彎曲振動(dòng)等。工程中常用靜平衡和動(dòng)平衡的方法來消除振動(dòng)。當(dāng)轉(zhuǎn)子的速度與臨界轉(zhuǎn)速接近時(shí),轉(zhuǎn)子將發(fā)生劇烈的振動(dòng)現(xiàn)象即共振,為防止共振,需要計(jì)算出轉(zhuǎn)子系統(tǒng)的固有頻率和臨界轉(zhuǎn)速,并且盡可能的使工作轉(zhuǎn)速遠(yuǎn)離臨界轉(zhuǎn)速。計(jì)算轉(zhuǎn)子固有頻率的方法有矩陣迭代法、傳遞矩陣法、特征方程法、特征值法、能量法等解析方法及ANSYS有限元模態(tài)分析法等[1-2]。
臥螺離心機(jī)結(jié)構(gòu)復(fù)雜,附件眾多,軸承跨距大,包括外轉(zhuǎn)子(轉(zhuǎn)鼓軸)和內(nèi)轉(zhuǎn)子(螺旋軸)兩個(gè)旋轉(zhuǎn)部件,本文先用ANSYS軟件分別建立內(nèi)外轉(zhuǎn)子的有限元模型進(jìn)行模態(tài)分析,并與傳遞矩陣法分析結(jié)果進(jìn)行比較,證明ANSYS分析方法的可靠性,再將內(nèi)外轉(zhuǎn)子耦合起來,進(jìn)行ANSYS模態(tài)分析,得出臥螺離心機(jī)整個(gè)旋轉(zhuǎn)系統(tǒng)的固有頻率和振型,為復(fù)雜機(jī)器設(shè)備的振動(dòng)特性分析提供一些參考。
1·臥螺離心機(jī)的主要結(jié)構(gòu)和工作原理
臥螺離心機(jī)的主要構(gòu)件有進(jìn)料管、轉(zhuǎn)鼓、螺旋推進(jìn)器、變速器、過載保護(hù)裝置、卸渣裝置等。如圖1所示,在機(jī)殼內(nèi)有兩個(gè)同心裝在主軸承上的回轉(zhuǎn)部件,外面是無孔轉(zhuǎn)鼓,里面是螺旋推進(jìn)器。主電動(dòng)機(jī)通過三角皮帶輪帶動(dòng)轉(zhuǎn)鼓旋轉(zhuǎn)。轉(zhuǎn)鼓通過左軸承處的空心軸與行星差速器的外殼相連接,行星差速器的輸出軸帶動(dòng)螺旋推進(jìn)器和轉(zhuǎn)鼓做同速轉(zhuǎn)動(dòng),但轉(zhuǎn)速不同,其轉(zhuǎn)差率一般為轉(zhuǎn)鼓轉(zhuǎn)速的0.2%~3%。懸浮液從右端的中心加料管連續(xù)送入機(jī)內(nèi),經(jīng)過螺旋推進(jìn)器的內(nèi)筒加料隔倉(cāng)的進(jìn)料孔進(jìn)到轉(zhuǎn)鼓內(nèi)。在離心力作用下沉降到轉(zhuǎn)鼓內(nèi)表面上而形成層渣,由于螺旋葉片與轉(zhuǎn)鼓的相對(duì)運(yùn)動(dòng),沉渣被螺旋葉片推送到轉(zhuǎn)鼓小端的干燥區(qū),從排渣孔甩出。在轉(zhuǎn)鼓的大端蓋上開設(shè)有若干溢流孔,澄清液便從此處流出,經(jīng)機(jī)殼的排液室排出。
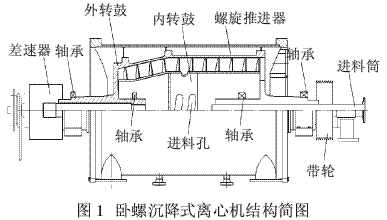
當(dāng)過載或螺旋推進(jìn)器意外卡住時(shí),位于機(jī)器最左端的過載保護(hù)裝置能自動(dòng)斷開主電動(dòng)機(jī)電源,停止進(jìn)料,防止事故發(fā)生。
2·轉(zhuǎn)子有限元分析基本原理
有限元分析中,將轉(zhuǎn)子看成由剛性圓盤和分布質(zhì)量彈性軸構(gòu)成,而滾動(dòng)軸承及軸承座以其等效剛性和阻尼的組合形式來表示其對(duì)轉(zhuǎn)子的作用力,該等效剛性和阻尼的具體值由經(jīng)驗(yàn)公式方法得出[3]。根據(jù)轉(zhuǎn)子動(dòng)力學(xué)有限元理論,在只考慮轉(zhuǎn)子橫向振動(dòng)的情況下,轉(zhuǎn)子系統(tǒng)的運(yùn)動(dòng)微分方程為:
[M]{ü}+[C]{u}+[K]{u}={Q}(1)
其中:[M]和[K]分別為系統(tǒng)的質(zhì)量矩陣和剛度矩陣;[C]為陀螺力[C]矩陣和阻尼力矩陣組合而成;{Q}為外力矢量。
當(dāng)沒有外力作用時(shí),即:{Q}=0時(shí)得到系統(tǒng)自由振動(dòng)方程,忽略阻尼力的影響,自由振動(dòng)方程為:
[M]{ü}+[K]{u}={0}(2)
假設(shè)結(jié)構(gòu)作如下簡(jiǎn)諧振動(dòng):
{X}={x}cos(wt)(3)
將式(3)代入式(2)中可得齊次方程:
([K]-ω2[M]){u}={0}(4)
這個(gè)方程的根為ω(i2i=1,2,3,…,n),即特征值,ωi(rad/s)為結(jié)構(gòu)的自然圓頻率,則自然頻率fi=ωi/2π。相應(yīng)的向量是{u}i,它表示振型,即假定結(jié)構(gòu)以fi振動(dòng)時(shí)的形狀。
3·轉(zhuǎn)鼓軸和螺旋軸的有限元模型
本文所研究的臥螺離心機(jī)是國(guó)內(nèi)廣泛應(yīng)用于PTA裝置的重型壓力離心機(jī),其轉(zhuǎn)鼓直徑為1 200 mm,轉(zhuǎn)鼓轉(zhuǎn)速為900 r/min,轉(zhuǎn)鼓壁厚為20 mm,主軸承跨距為3 400 mm,分離因素為543.3,轉(zhuǎn)鼓半錐角為9.875°,為方便分析,先將其結(jié)構(gòu)進(jìn)行簡(jiǎn)化,簡(jiǎn)化原理如下[4]:
(1)忽略零件之間的螺栓連接,認(rèn)為由螺栓連接起來的部件是一個(gè)整體,忽略倒角。其中從動(dòng)法蘭、出料端轉(zhuǎn)子頭、錐形轉(zhuǎn)子、水平轉(zhuǎn)子及供料端轉(zhuǎn)子頭組成了轉(zhuǎn)鼓軸系統(tǒng)。傳動(dòng)軸和螺旋推進(jìn)器組成了螺旋軸系統(tǒng)。 (2)將螺旋推進(jìn)器上的螺旋葉片簡(jiǎn)化為質(zhì)量點(diǎn),將其上的進(jìn)料孔等效為負(fù)質(zhì)量,軸承簡(jiǎn)化為支撐,其余部分簡(jiǎn)化為軸。
(3)忽略陀螺力矩和阻尼力的影響。
螺旋推進(jìn)器上的螺旋葉片簡(jiǎn)化為質(zhì)量點(diǎn)加載在筒體上。錐螺旋葉片的質(zhì)量用PROE建模讀取質(zhì)量M=91.27 kg,將其視為一個(gè)質(zhì)量點(diǎn)加載在ANSYS錐部模型的中點(diǎn)處。柱螺旋葉片的質(zhì)量用PROE建模讀取質(zhì)量M=263.63 kg,將其平均分為四個(gè)質(zhì)量點(diǎn)(m=65.91kg)均勻加載在柱筒上。錐螺旋葉片和柱狀螺旋葉片如圖2所示。
分析中軸采用Beam188梁?jiǎn)卧M(jìn)行模擬,軸承用COMBI214單元模擬,質(zhì)量點(diǎn)用MASS21單元模擬。轉(zhuǎn)鼓軸和螺旋軸的ANSYS有限元模型如圖3、4所示。

4·模態(tài)分析
4.1實(shí)常數(shù)的選取
分析中,取彈性模量E為2.1×1011 N/m2,泊松比μ為0.3,密度ρ為7 960 kg/m3,臥螺離心機(jī)旋轉(zhuǎn)部件由四個(gè)軸承支撐,其中螺旋軸左右兩端均有軸承將其支撐在轉(zhuǎn)鼓軸上,轉(zhuǎn)鼓軸左右兩端的兩軸承將整個(gè)旋轉(zhuǎn)部件支撐于機(jī)架上。螺旋軸兩端的軸承剛度分別為1.87×108 N/m和4.85×108 N/m,轉(zhuǎn)鼓軸兩端的軸承剛度分別為2.09×108 N/m和2.41×108 N/m[4]。
4.2模態(tài)分析結(jié)果
通用有限元軟件ANSYS提供了七種模態(tài)分析求解的方法。即:Subspace法、Block Lanczos法、Power-Dynamics法、Reduced法、Unsymmertic法、Damp法和QR Damp法。本分析采用Lanczos法計(jì)算轉(zhuǎn)鼓軸和螺旋軸的前兩階固有頻率,計(jì)算結(jié)果如表1所示。
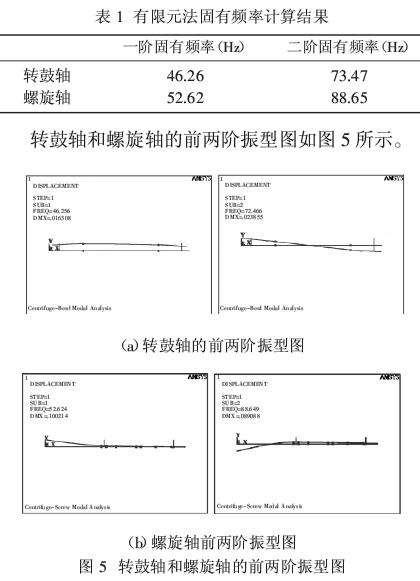
5·傳遞矩陣法計(jì)算結(jié)果
傳遞矩陣法是工程上用于計(jì)算轉(zhuǎn)子系統(tǒng)臨界轉(zhuǎn)速和不平衡響應(yīng)等的主要近似數(shù)值方法之一,傳遞矩陣法發(fā)展較完善,計(jì)算時(shí)取轉(zhuǎn)子為集中質(zhì)量或分布質(zhì)量模型[5],本文中采用分布質(zhì)量模型,將軸分為若干個(gè)等截面軸段,同時(shí)計(jì)入軸段的轉(zhuǎn)動(dòng)慣量和剪切變形。分布質(zhì)量傳遞矩陣計(jì)算軸的橫向彎曲振動(dòng)精度高,可按軸的實(shí)際情況而分段,精度不受分段段數(shù)的影響。
轉(zhuǎn)鼓軸與螺旋軸的分布質(zhì)量傳遞矩陣法的計(jì)算模型如圖6所示。
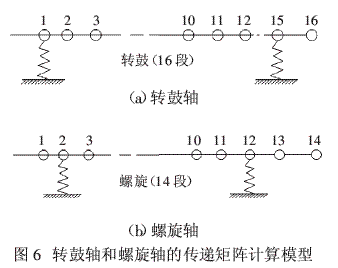
轉(zhuǎn)鼓軸和螺旋軸的傳遞矩陣法固有頻率計(jì)算結(jié)果如表2所示。

將傳遞矩陣法計(jì)算結(jié)果與ANSYS有限元計(jì)算結(jié)果相比較,誤差都在5%以內(nèi),兩種算法的結(jié)果基本一致,從而驗(yàn)證了ANSYS分析結(jié)果的正確性,為耦合雙軸系統(tǒng)固有頻率的計(jì)算提供比較簡(jiǎn)便的分析方法。
6·耦合雙軸系統(tǒng)ANSYS計(jì)算結(jié)果
用COMBI214彈簧單元將轉(zhuǎn)鼓軸和螺旋軸連接起來形成耦合雙軸系統(tǒng),由ANSYS模態(tài)分析得出前兩階固有頻率和振型。雙軸系統(tǒng)有限元模型及前兩階振型圖如圖7、圖8所示。
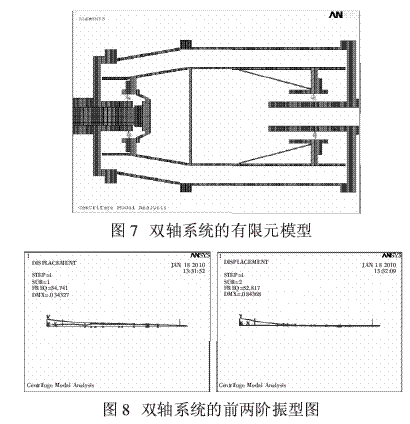
結(jié)果顯示雙軸系統(tǒng)的一階固有頻率為34.74 HZ,一階臨界轉(zhuǎn)速為2 084 r/min,二階固有頻率為52.82HZ,二階臨界轉(zhuǎn)速為3 169 r/min,而本文所研究臥螺離心機(jī)轉(zhuǎn)鼓的工作轉(zhuǎn)速為900 r/min,遠(yuǎn)遠(yuǎn)小于一階臨界轉(zhuǎn)速,因此,在正常轉(zhuǎn)速范圍內(nèi),機(jī)器不會(huì)發(fā)生共振現(xiàn)象。
7·結(jié)論
通過大型通用ANSYS有限元軟件建模計(jì)算得出臥式螺旋卸料沉降式離心機(jī)耦合雙軸系統(tǒng)的固有頻率和振型,結(jié)果表明機(jī)器在正常工作轉(zhuǎn)速下不會(huì)發(fā)生共振。此種ANSYS分析方法的建模方便,求解速度快,通用性好,為其它雙軸系統(tǒng)甚至是多軸系統(tǒng)旋轉(zhuǎn)機(jī)械的振動(dòng)特性分析提供了一定的參考。
參考文獻(xiàn):
[1]鐘一諤,何衍宗,王正,等.轉(zhuǎn)子動(dòng)力學(xué)[M].北京:清華大學(xué)出版社,1987.
[2]董俊華,范德順.臥式螺旋離心機(jī)的轉(zhuǎn)鼓與螺旋輸送器的有限元分析[D].北京:北京化工大學(xué)機(jī)電工程學(xué)院,2004.
[3]孫紅巖,張小龍.基于ANSYS軟件的轉(zhuǎn)子系統(tǒng)臨界轉(zhuǎn)速及模態(tài)分析[J].機(jī)械制造與研究,2008,37(4):53-54.
[4]張曉軍,張志新,賀世正,楊健.臥螺離心機(jī)轉(zhuǎn)子動(dòng)力特性計(jì)算[J].流體機(jī)械,2007,35(5):47-49.
[5]張小龍,何洪慶.渦輪泵轉(zhuǎn)子的臨界轉(zhuǎn)速研究(Ⅳ)分布質(zhì)量軸的傳遞矩陣法[J].推進(jìn)技術(shù),2000,21(2):52-55.
標(biāo)簽:
相關(guān)技術(shù)
2、如涉及作品內(nèi)容、版權(quán)和其它問題,請(qǐng)?jiān)?0日內(nèi)與本網(wǎng)聯(lián)系,我們將在第一時(shí)間作出適當(dāng)處理!有關(guān)作品版權(quán)事宜請(qǐng)聯(lián)系:+86-571-88970062
- 2025年一季度通用機(jī)械行業(yè)企業(yè)動(dòng)態(tài)匯總
- 浙江省抽查100批次閥門產(chǎn)品,7批次不合格
- 江蘇省緊固件行業(yè)協(xié)會(huì)召開常務(wù)理事擴(kuò)大會(huì)議
- 德國(guó)波勒過濾器公司采購(gòu)總監(jiān)Sabine Stejskal一行蒞臨艾坦姆合金調(diào)研考察
- 聊城軸承小鎮(zhèn)的“智造”先鋒:華工軸承的成長(zhǎng)啟示
- 西北軸承鐵路車間開展現(xiàn)場(chǎng)優(yōu)化專項(xiàng)行動(dòng)
- 我國(guó)最大超深油田油氣產(chǎn)量當(dāng)量累計(jì)超2000萬噸
- 百萬噸級(jí)!我國(guó)首個(gè)海上CCUS項(xiàng)目開鉆
- 陜鼓簽約百萬噸CCUS示范項(xiàng)目
- 瓦軸集團(tuán)智慧攻堅(jiān) 巧解生產(chǎn)難題
- 國(guó)際事業(yè)公司駐緬機(jī)構(gòu)全力保障緬甸災(zāi)區(qū)用油
- 中油測(cè)井自主研發(fā)新技術(shù)煤中“淘”氣