TBS全自動離心機刮鏟卸料裝置的動態(tài)特性分析

                        楊普國1，2，劉泓濱1，陳俊2

　　（1.昆明理工大學機電工程學院，云南昆明650039；2.昆明冶金高等專科學校電氣學院，云南昆明650033）

　　摘要：通過對TBS全自動間隙離心機刮鏟裝置在生產過程出現的問題進行分析；采用用戶自定義矩陣單元來處理刮鏟裝置結合部的接觸問題，在Pro/E軟件上建立了刮鏟裝置“Z”軸的有限元模型，并對其進行了動態(tài)特性分析。運用該方法來進行結構的性能預測，并用于工廠對該裝置的結構進行改進設計。

　　 關鍵詞：刮鏟裝置；有限元；動態(tài)特性

　　中圖分類號：TH122文獻標識碼：A doi:10.3969/j.issn.1002-6673.2010.05.018
　　文章編號：1002－6673（2010）05－047－03

　　0·引言

　　TBS全自動離心機是從國外引進的全自動篩分設備。主要應用于化工、石油、食品、制藥、選礦、煤炭、水處理和船舶等部門。隨著糖廠生產自動化水平的提高，對設備的要求也越來越高。在篩分工段，其最基本的問題要求提高全自動離心機的工作性能。離心機刮鏟裝置工作性能決定了全自動離心機的工作性能。而刮鏟裝置的工作性能是與其動態(tài)性能緊密相關的。近年來，由于現代設計方法的廣泛應用，對刮鏟裝置“Z”軸進行動態(tài)特性分析，用動態(tài)設計取代靜態(tài)設計已成為現代設計的必然趨勢。

　　刮鏟裝置是由多個零部件組成的復雜組合結構，僅對個別零部件進行分析，無法全面反映刮鏟裝置的整體性能，特別是在動態(tài)分析中，各零部件之間結合部的接觸參數對動態(tài)性能的解析計算精度影響很大，因此，要準確地預測刮鏟裝置的動態(tài)性能，就必須對整個裝置進行動力學分析。

　　有限元法是對每個單元取假設模態(tài)，由于單元的數目通常比較大，假設模態(tài)就可以取得非常簡單，而且它以節(jié)點位移作為系統的廣義坐標，可以降低系統微分方程的耦合程度，給用計算機求解帶來方便，所以，有限元法已成為分析復雜結構的有效方法和手段[2]。下面就采用有限元法在Pro/E軟件上建立了刮鏟裝置“Z”軸的有限元模型，并進行動態(tài)分析，并獲得試驗驗證。

　　1·刮鏟臂“Z”軸有限元模型的建立

　　刮鏟臂“Z”軸的有限元網格是在Pro/E軟件上建立的，首先建立刮鏟臂“Z”軸的幾何模型，如圖1所示，生成各零件的有限元網格。然后將各零件的有限元網格“裝配”在一起，就形成整個裝置的有限元網格。

　　將Pro/E軟件上生成的有限元網格轉至ANSYS軟件中，以用于作動力學分析，結合部采用適當的聯接單元聯接，再按實際位置施加位移邊界條件。2刮鏟臂“Z”軸的結合部接觸問題的處理聯接處的結合條件對結構性特別是動態(tài)性能的影響很大。要想建立一個精確的組合結構動力學模型，進行結構的動態(tài)設計與動力學分析，如何正確處理結合部的接觸問題是關鍵技術之一。

　　在用有限元法進行結構動力學分析時，可取節(jié)點位移為廣義坐標，在建立了單元的位移函數后，單元的動能T和勢能V可表示為：

              

　　式中：{q}、{F}—分別為總體節(jié)點位移和載荷列陣；[M]、[C]、[K]—分別為系統的質量矩陣、阻尼矩陣和剛度矩陣。

　　若結構中有附加質量，彈性聯接和接觸阻尼，就需要對系統的能量和載荷進行修正。為此，采用一種用戶自定義矩陣單元（剛度矩陣、阻尼矩陣或質量矩陣）來處理這個問題。該單元無需定義幾何形狀，只要給出矩陣元素值，即可聯接空間的任意兩個節(jié)點，每個節(jié)點有六個自由度，則該單元就有12個自由度，如圖2所示。

               

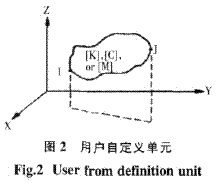
　　由式（1）~（3）可知，在節(jié)點間加入自定義的剛度矩陣單元、阻尼矩陣單元和質量矩陣單元，只要矩陣元素取適當的值，就可以在系統的能量和載荷計算中，計入由于接觸剛度帶來的勢能，接觸阻尼引起的阻尼力和附加質量引起的動能。刮產卸料裝置在工作中存在著接觸剛度和接觸阻尼，這些參數可通過在工作中和試驗分析獲得。在具體應用中，可以采用用戶定義的剛度矩陣和阻尼矩陣單元來處理，由于剛度矩陣和阻尼矩陣都是對稱矩陣，則有78個獨立元素。

                 

　　例如，若已知兩節(jié)點之間只有X方向的聯接剛度K，根據剛度的物理意義，可求得剛度矩陣單元中的元素取值應為：C1=-C7=C58=K，其余為零。阻尼矩陣單元的元素求值方法類似。
　　由此可以看出，通過對剛度矩陣單元和阻尼矩陣單元的元素取不同的值，就能描述兩節(jié)點間的各種聯接情況，其它形式的聯接單元（如軟件中的彈簧元、阻尼元）也均可采用這種單元來代替，因此用戶自定義矩陣單元可以作為一種通用的聯接單元來使用。

　　3·刮鏟裝置的動態(tài)特性分析

　　刮鏟裝置的動態(tài)特性分析是在ANSYS軟件上進行的，采用“Z”軸進行模態(tài)分析。由此可得刮鏟臂在這三個方向上的優(yōu)勢固有頻率，與試驗值比較，相對誤差均在17%以內，見表1。

　　由于刮鏟臂下端部與刮刀相連，其動態(tài)響應直接影響刮鏟裝置的精度。為此采用了模態(tài)疊加法進行了頻普響應分析，求得刮鏟臂下端部中心點X、Y、Z三個方向的動柔度幅值曲線如圖3所示。對應于各方向優(yōu)勢固有頻率處的動柔度幅值見表2[14]。

　　4·結束語

　　由計算結果可知，除了Y方向在第一階優(yōu)勢固有頻率處的動柔度幅值略小外，該刮鏟裝置在X、Y兩個方瞬時流量之和，而每個子泵的瞬時流量計算同于普通外嚙合齒輪泵，所以有:

                 

　　式中：R1、R2分別為主、從動齒輪的節(jié)圓半徑；h1、h2分別為主、從動齒輪的齒頂高；ω—主動齒輪的角速度，ω=2πn；f為嚙合點到節(jié)點的距離，f=Rf1φ，Rf1為主動齒輪的基圓半徑；φ—主動齒輪的轉角。

　　由上式可知，齒輪泵的瞬時流量隨著嚙合點到節(jié)點距離的變化而變化，f愈大時，Qsh愈小。所以當兩齒開始進入嚙合或退出嚙合時，泵的流量最小；當嚙合點在節(jié)點處時，Qsh最大。齒輪嚙合時嚙合點距的變化，是由齒輪嚙合傳動的特點所決定的，是不可避免的。所以對于只具有一對齒輪的普通齒輪泵，其較大的輸出流量脈動，也就成了必然，使泵的應用范圍受到了限制。但對于具有兩對齒輪嚙合的平面式并聯齒輪泵來說，在每一瞬時，每個子泵中至少有一對輪齒處于嚙合狀態(tài)，其輸出流量的脈動情況，取決于兩子泵的嚙合點距的相位變化情況。若能使兩子泵的嚙合點距的變化相位不同，則可使兩子泵的瞬時流量的極大和極小值交替出現，相互迭加的結果即可大大減少泵的輸出流量脈動。嚙合點距的相位變化取決于齒數的選擇[3]。另外，增加齒輪的齒數時，也可減少流動脈量幅度[4]。

　　 4·結論

　　根據上述分析可見，平面式并聯齒輪泵在一般情況下具有徑向力平衡、流量比同結構尺寸的齒輪泵大、流量脈動小等特點，從而彌補了普通外嚙合齒輪泵的一些不足之處。從并聯齒輪泵的結構和性能上的理論分析來看，由于它所受的徑向力大大地減少，甚至平衡，因此產生的磨損小，可以大大地提高泵的壽命及容積效率。但多齒輪泵的制造價格遠比普通的外嚙合齒輪泵高，安裝精度也高。因此，多齒輪泵還須在泵的具體結構設計、加工制造工藝和材料選用等方面做進一步的探索和實驗，以便能使其盡早地應用于更多的工業(yè)領域。

參考文獻:

[1]楊平，葛云.液壓液力與氣壓傳動[M].北京：科學出版社，2007.

[2]何存興.液壓元件[M].北京：機械工業(yè)出版社，1985.

[3]候波.二從動輪式復合齒輪泵的流量特性[J].安徽理工大學學報，2004，3.

[4]夏立中.非對稱漸開線多齒輪泵的理論分析[J].東北煤礦技術，1997，1.