泵軸臨界轉(zhuǎn)速的基本概念
軸臨界轉(zhuǎn)速的基本概念
泵軸除校核強(qiáng)度外,要進(jìn)行剛度計(jì)算。剛度計(jì)算包括兩部分內(nèi)容:第一是計(jì)算軸的撓度,使軸在運(yùn)轉(zhuǎn)中的撓度小于轉(zhuǎn)子和殼體間的平徑間隙。軸運(yùn)轉(zhuǎn)中的撓度等于轉(zhuǎn)子自重引起的靜撓度,加土殘余不平衡質(zhì)量的離心慣性力引起的動(dòng)撓度。但是精確地確定轉(zhuǎn)子的殘余不平衡質(zhì)覺(jué)及位置是很困難的,所以一般只用轉(zhuǎn)子自敢引起的靜撓度,作為近似的比較標(biāo)準(zhǔn)。第二是一計(jì)算軸的臨界轉(zhuǎn)速.以保證轉(zhuǎn)子的平穩(wěn)運(yùn)轉(zhuǎn)。

共振和臨界轉(zhuǎn)速
觀察旋轉(zhuǎn)中的軸,可以發(fā)現(xiàn),當(dāng)軸的轉(zhuǎn)速由啟動(dòng)增加到某一轉(zhuǎn)速時(shí),軸運(yùn)轉(zhuǎn)變?yōu)椴环€(wěn)定,產(chǎn)生較強(qiáng)烈的反復(fù)變形和振動(dòng)。可是,如果繼續(xù)升高軸轉(zhuǎn)速,會(huì)連續(xù)反復(fù)出現(xiàn)上述現(xiàn)象,我們稱(chēng)這種現(xiàn)象為共振現(xiàn)象,產(chǎn)生共振的轉(zhuǎn)速稱(chēng)為軸的臨界轉(zhuǎn)速。引起第一次共振的轉(zhuǎn)速稱(chēng)為第一臨界轉(zhuǎn)速,引起第二次共振的轉(zhuǎn)速稱(chēng)為第二臨界轉(zhuǎn)速,以此類(lèi)推。
我們主要研究第一臨界轉(zhuǎn)速。
下面,對(duì)上述現(xiàn)象作簡(jiǎn)單的理論分析,以便了解臨界轉(zhuǎn)速的實(shí)質(zhì)和決定臨界轉(zhuǎn)速的主要因素。
圖21--23表示的是質(zhì)量為m的圓盤(pán),裝在兩支點(diǎn)的垂直軸中間,以角速度。旋轉(zhuǎn)時(shí)的狀態(tài)。為研究方便,不計(jì)軸本身的質(zhì)量,圖中O表示軸心一軸承連線(xiàn)和圓盤(pán)的交點(diǎn),O1表示幾何中心一圓盤(pán)兒何對(duì)稱(chēng)中心與軸心的交點(diǎn).O2表示圓盤(pán)的重心。由于材料的質(zhì)量不均勻和不可能做到理想平衡等原因,圓盤(pán)重心O2與幾何中心O1不重合,其偏心距用。表示。
因?yàn)檩S垂直放置,所以當(dāng)軸靜止時(shí),軸心線(xiàn)與軸承連線(xiàn)重合,軸不產(chǎn)生擾度;當(dāng)軸開(kāi)始旋轉(zhuǎn)時(shí),因?yàn)橛衅膃,則圓盤(pán)重心O2,以偏心距e為平徑繞軸承連線(xiàn)作圓周運(yùn)動(dòng)。由此產(chǎn)生的離心慣性力使軸變形,引起動(dòng)擾度yd。所以軸旋轉(zhuǎn)起來(lái)之后其圓盤(pán)重心O2,是以半徑r- e+ yd繞軸承連線(xiàn)作圓周運(yùn)動(dòng)。這時(shí)作用在圓盤(pán)上的離心慣性力為
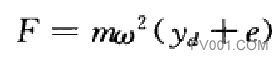
式中m-一圓盤(pán)的質(zhì)量,kg;
w--一軸旋轉(zhuǎn)的角速度,rad/s;
yd一動(dòng)繞度,m
軸變形后,在軸內(nèi)產(chǎn)生抵抗變形的內(nèi)力,此力為軸的彈性力,用P表示。在彈性限度內(nèi),軸的彈性力與擾度yd(變形)成正比,即P =Kyd
K稱(chēng)為軸的剛性系數(shù),是軸產(chǎn)生單位變形的彈性力(N/m)。其值表示軸的剛度大小。K值與軸的材料、尺寸、支撐特點(diǎn)和載荷分布等因數(shù)有關(guān)。
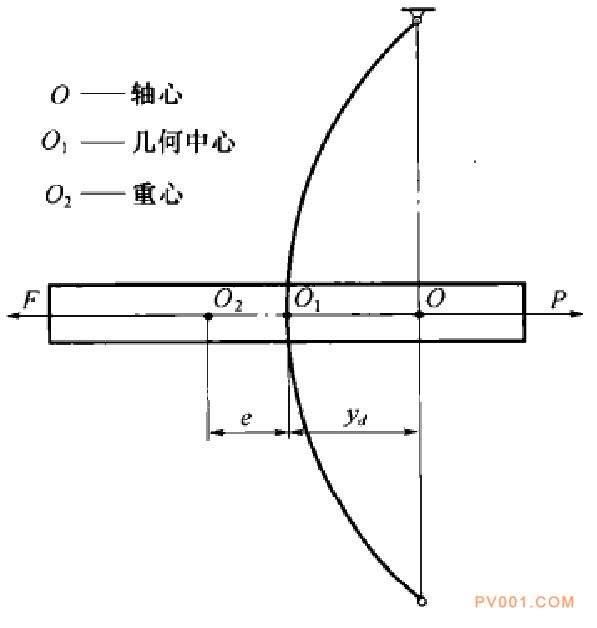
圖21一23 垂直軸裝單圓盤(pán)轉(zhuǎn)子的轉(zhuǎn)動(dòng)情況
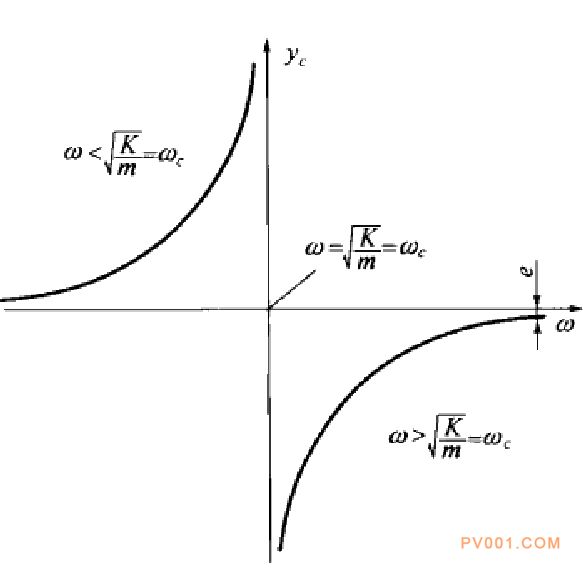
圖21一24 軸擾度y與角速度w的關(guān)系
離心慣性力F的作用是力圖增加軸的擾度,使軸產(chǎn)生變形,增加偏心e而彈性力p是力圖減小軸的擾度,恢復(fù)原來(lái)的形狀。在平衡狀態(tài)下,離心慣性力與所有擾度下的軸的彈性力相平衡。即兩力大小相等,方向相反。由平衡條件可以寫(xiě)成
對(duì)于給定的軸e、K、m為定值,故擾度yd隨角速度。而變化。取yd為縱坐標(biāo),w為橫坐標(biāo),按公式畫(huà)出兩者的關(guān)系曲線(xiàn),如圖21一24所示。
式(21---25)表面上看是yd和w的關(guān)系式。實(shí)際上它是反映了離心慣性力和彈性力的平衡口顯然w。代表平衡的一方—離心慣性力;為代表平衡的另一方—軸的彈性力。
隨著w的增加,在不同的發(fā)展階段,離心慣性力和軸的彈性力有不同的表現(xiàn)形式,而反映出軸有不同的變形(擾度)的特性.
(1)當(dāng)w=0時(shí),因軸不旋轉(zhuǎn),所以為yd=0,圓盤(pán)中心O1在軸承連線(xiàn)上,與軸心O相重合,與重心佼的距離為e幾何重心O1重心O2與軸心O的關(guān)系如圖21-25〔a)所示。
(2)當(dāng)w從O逐漸增加,在上式的分母沒(méi)有變成負(fù)值之前,yd為正值,且隨著。的增加而增大。在此階段內(nèi),軸在所有擾度下,彈性力和離心慣性力相平衡。幾何中心O1重心O2與軸心O的關(guān)系如圖21一25 (b)所示。
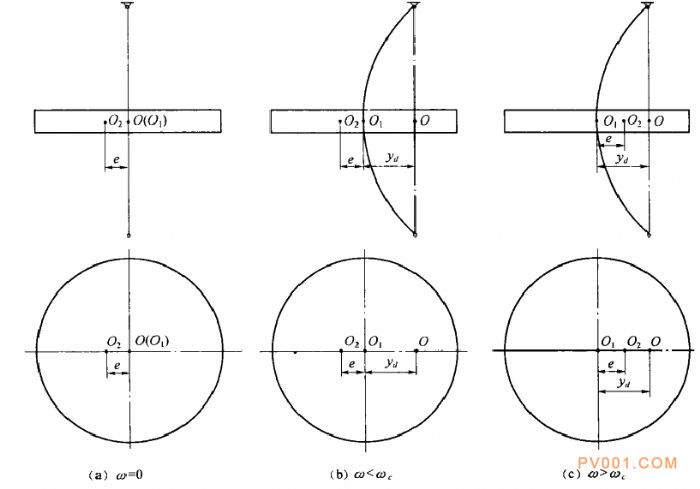
圖21一25 不同轉(zhuǎn)速下圓盤(pán)幾何中心O1重心O2與軸心O的位置關(guān)系
標(biāo)簽:
相關(guān)技術(shù)
2、如涉及作品內(nèi)容、版權(quán)和其它問(wèn)題,請(qǐng)?jiān)?0日內(nèi)與本網(wǎng)聯(lián)系,我們將在第一時(shí)間作出適當(dāng)處理!有關(guān)作品版權(quán)事宜請(qǐng)聯(lián)系:+86-571-88970062
- 2025年一季度通用機(jī)械行業(yè)企業(yè)動(dòng)態(tài)匯總
- 浙江省抽查100批次閥門(mén)產(chǎn)品,7批次不合格
- 江蘇省緊固件行業(yè)協(xié)會(huì)召開(kāi)常務(wù)理事擴(kuò)大會(huì)議
- 德國(guó)波勒過(guò)濾器公司采購(gòu)總監(jiān)Sabine Stejskal一行蒞臨艾坦姆合金調(diào)研考察
- 聊城軸承小鎮(zhèn)的“智造”先鋒:華工軸承的成長(zhǎng)啟示
- 西北軸承鐵路車(chē)間開(kāi)展現(xiàn)場(chǎng)優(yōu)化專(zhuān)項(xiàng)行動(dòng)
- 我國(guó)最大超深油田油氣產(chǎn)量當(dāng)量累計(jì)超2000萬(wàn)噸
- 百萬(wàn)噸級(jí)!我國(guó)首個(gè)海上CCUS項(xiàng)目開(kāi)鉆
- 陜鼓簽約百萬(wàn)噸CCUS示范項(xiàng)目
- 瓦軸集團(tuán)智慧攻堅(jiān) 巧解生產(chǎn)難題
- 國(guó)際事業(yè)公司駐緬機(jī)構(gòu)全力保障緬甸災(zāi)區(qū)用油
- 中油測(cè)井自主研發(fā)新技術(shù)煤中“淘”氣